Thin Walled Pressure Vessel CE 213 Solid Mechanics

Thin Walled Pressure Vessel

Thin wall pressure vessels (TWPV) are widely used in industry for storage and transportation of

liquids and gases when configured as tanks. They also appear as components of aerospace and marine vehicles

such as rocket and balloon skins and submarine hulls (although in the latter case the vessel is externally

pressurized, violating one of the assumptions listed below).

Two geometries will be examined in this lecture:

• Cylindrical pressure vessels.

• Spherical pressure vessels.

The walls of an ideal thin-wall pressure vessel act as a membrane (that is, they are unaffected by

bending stresses over most of their extent). A sphere is the optimal geometry for a closed pressure vessel in the

sense of being the most structurally efficient shape. A cylindrical vessel is somewhat less efficient for two

reasons: (1) the wall stresses vary with direction, (2) closure by end caps can alter significantly the ideal

membrane state, requiring additional local reinforcements. However the cylindrical shape may be more

convenient to fabricate and transport.

Assumptions

The key assumptions used here are: wall thinness and geometric symmetries. These make possible to

obtain average wall stresses analysis with simple free-body diagrams (FBD). Here is a more detailed list of

assumptions:

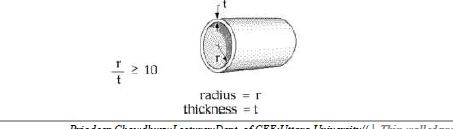
1. Wall Thinness.The wall is assumed to be very thin compared to the other dimensions of the vessel. If the 

thickness is t and a characteristic dimension is R (for example, the radius of the cylinder or sphere) we assume

that

t/R << 1, or R/t >> 1 ;Usually R/t > 10.

As a result, we may assume that the stresses are uniform across the wall.

2. Symmetries. In cylindrical vessels, the geometry and the loading are cylindrically symmetric. Consequently

the stresses may be assumed to be independent of the angular coordinate of the cylindrically coordinate system.

In spherical vessels, the geometry and the loading are spherically symmetric. Therefore the stresses may be

assumed to be independent of the two angular coordinates of the spherical coordinate system and in fact are the

same in all directions.

3. Uniform Internal Pressure. The internal pressure, denoted by p, is uniform and everywhere positive. If the

vessel is also externally pressurized, for example subject to atmospheric pressure, p is defined by subtracting the

external pressure from the internal one, a difference called gage pressure. If the external pressure is higher, as in

the case of a submarine hull, the stress formulas should be applied with extreme caution because another failure

mode: instability due to wall buckling may come into play.

4. Ignoring End Effects. Features that may affect the symmetry assumptions are ignored. This includes

supports and cylinder end caps. The assumption is that disturbances of the basic stress state are confined to local

regions and may be ignored in basic design decision such as picking up the thickness away from such regions.

Pressure Filled Cylinder

To begin our investigation of pressure vessels, let’s consider the internally pressurized cylinder shown

below

First, we take a plane which is normal to the axis of the cylinder and use it to create an imaginary cut in

the cylinder.That is the vertical cut and we will obtain the vertical cut plane.(look at the fig carefully)

After cutting the cylinder, we retain the back half of the cylinder. Remember, since this was an imaginary cut,

the gas in the remaining half of the cylinder does not escape. This portion of the cylinder is still pressurized!

The cylinder has a thickness, t, and a radius, r. This analysis is limited to "Thin Walled Pressure

Vessels". For a cylinder to qualify as "thin walled" the ratio of radius to thickness (r/t) must be at least 10..

The internal pressure, which is still acting on this portion of the cylinder, is represented in the pressure

field shown below. The pressure is constant over the entire cut of the cylinder. Note that we draw the pressure in

a manner which tends to inflate the cylinder. If the pressure acts in the opposite sense to that shown below, the

following analysis must be used with caution. When we load vessels with "external pressure" the loading can

result in buckling (crumpling) of the cylinder

In order for the free-body diagram to satisfy equilibrium, there must be some force which counteracts

the internal pressure. When analyzing thin walled pressure vessels it is assumed that all stresses act parallel to

the surface of the vessel. This is often called "membrane action". In the cylinder below, the only stress acting on

the cut which can counteract the internal pressure is the normal stress σ

At this point we have enough information to apply force equilibrium in the longitudinal direction. The

figure above represents the fact that the force caused by the internal pressure must be equilibrated by the force

caused by the longitudinal normal stress.

Remember, stress (and pressure) is expressed in units of force over area. To include stresses (and

pressures) in force equilibrium equations, you must multiply the stress (or pressure) times the area on which it

acts. The areas acted on by the longitudinal stress and the pressure are calculated in the figure above.

Once we have figured the areas, we can calculate the forces caused by the pressure and the normal stress

as shown bellow

Equilibrium requires that the two forces be equal if the cylinder is to remain stationary. So from the

equation above,

We call this stress in a cylinder the "longitudinal stress" because it acts parallel to the long axis of the

cylinder.

We just calculated the longitudinal stress. Is this the only stress acting in a pressure filled cylinder? Let's

cut the cylinder in a different manner and see. This time our cut is parallel to the axis of the cylinder.

After the cut we retain the bottom half of the cylinder. Again, the gas has not left the portion of the

cylinder shown above: it is still pressurized.

But our cutting does not stop there. Next, we remove a slice of the cylinder which is of length Δl.

What remains after our slicing and dicing is a "half pipe" of length Δl. Our previous analysis addressed

the pressure which acts on this element in the longitudinal direction, what other pressure would act on the

vessel.

This time we will look at the pressure acting on the element in
the vertical direction. Again, as we have

drawn it the pressure tends to inflate the element.

The only stress acting in the vertical direction which can counteract the pressure shown on the previous

page is the normal stress σ1. This stress is called the "Hoop stress" because it acts like a steel hoop around a

wooden barrel.

It is time again to enforce equilibrium. Here we are focusing on forces which act in the vertical

direction.