Idealized Structure Part 1 CE 213 UGS

Idealized Structure
An exact analysis of a structure can never be carried out, since estimates
always have to be made of the loadings and the strength of the
materials composing the structure. Furthermore, points of application
for the loadings must also be estimated. It is important, therefore,
that the structural engineer develop the ability to model or idealize a
structure so that he or she can perform a practical force analysis of the
members. In this section we will develop the basic techniques necessary

to do this.







Support Connections. Structural members are joined together in
various ways depending on the intent of the designer.The three types of
joints most often specified are the pin connection, the roller support, and
the fixed joint. A pin-connected joint and a roller support allow some
freedom for slight rotation, whereas a fixed joint allows no relative rotation
between the connected members and is consequently more expensive to
fabricate. Examples of these joints, fashioned in metal and concrete, are
shown in Figs. 2–1 and 2–2, respectively. For most timber structures, the
members are assumed to be pin connected, since bolting or nailing them
will not sufficiently restrain them from rotating with respect to each other.
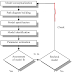
Idealized models used in structural analysis that represent pinned and
fixed supports and pin-connected and fixed-connected joints are shown
in Figs. 2–3a and 2–3b. In reality, however, all connections exhibit some
stiffness toward joint rotations, owing to friction and material behavior.
In this case a more appropriate model for a support or joint might be
that shown in Fig. 2–3c. If the torsional spring constant the joint is
a pin, and if k : q, the joint is fixed.
k = 0













When selecting a particular model for each support or joint, the engineer
must be aware of how the assumptions will affect the actual performance
of the member and whether the assumptions are reasonable for the
structural design. For example, consider the beam shown in Fig. 2–4a,
which is used to support a concentrated load P. The angle connection at
support A is like that in Fig. 2–1a and can therefore be idealized as a
typical pin support. Furthermore, the support at B provides an approximate
point of smooth contact and so it can be idealized as a roller.The beam’s
thickness can be neglected since it is small in comparison to the beam’s
length, and therefore the idealized model of the beam is as shown in
Fig. 2–4b.The analysis of the loadings in this beam should give results that
closely approximate the loadings in the actual beam.To show that the model
is appropriate, consider a specific case of a beam made of steel with P = 8 k
(8000 lb) and One of the major simplifications made here was
assuming the support at A to be a pin. Design of the beam using standard
code procedures* indicates that a W would be adequate for
supporting the load. Using one of the deflection methods of Chapter 8, the
rotation at the “pin” support can be calculated as
From Fig. 2–4c, such a rotation only moves the top or bottom flange a
distance of This small
amount would certainly be accommodated by the connection fabricated as
shown in Fig. 2–1a, and therefore the pin serves as an appropriate model.
¢ = ur = 10.0103 rad215.12 in.2 = 0.0528 in.!
u = 0.0103 rad = 0.59°.
10 * 19







Other types of connections most commonly encountered on coplanar
structures are given in Table 2–1. It is important to be able to recognize
the symbols for these connections and the kinds of reactions they exert
on their attached members. This can easily be done by noting how the
connection prevents any degree of freedom or displacement of the
member. In particular, the support will develop a force on the member if
it prevents translation of the member, and it will develop a moment if it
prevents rotation of the member. For example, a member in contact
with a smooth surface (3) is prevented from translating only in one
direction, which is perpendicular or normal to the surface. Hence, the
surface exerts only a normal force F on the member in this direction.
The magnitude of this force represents one unknown. Also note that the
member is free to rotate on the surface, so that a moment cannot be
developed by the surface on the member. As another example, the fixed
support (7) prevents both translation and rotation of a member at the
point of connection. Therefore, this type of support exerts two force
components and a moment on the member. The “curl” of the moment
lies in the plane of the page, since rotation is prevented in that plane.
Hence, there are three unknowns at a fixed support.
In reality, all supports actually exert distributed surface loads on their
contacting members. The concentrated forces and moments shown in
Table 2–1 represent the resultants of these load distributions. This
representation is, of course, an idealization; however, it is used here since
the surface area over which the distributed load acts is considerably
smaller than the total surface area of the connecting members.