Static Bending Moment OF Timber Beam Lab Report CE 211

STATIC BENDING TEST OF TIMBER BEAM

1. OBJECTIVES

-To observe the bending behavior of beams with different moment of inertia (I).

-To determine the Modulus of Elasticity (E) of wood by conducting bending test.

- To evaluate the deflection of beam w.r.t. load increament. -To evaluate the failure patterns due to bending.

2. ASTM REFERENCE

ASTM D143 Standard Test Methods for Small Clear Specimens of Timber

3. SIGNIFICANCE

This experiment provides fundamental knowledge on bending behaviour of materials specially timber beam, test procedure, universal testing machine and its working principal, bending specimens, failure patterns etc.

4. APPARATUS

Universal Testing Machine (UTM), strain gauge or deflectometer, Support attaching system, steel tape, stop watch and computer.

5. SPECIMENS Timber beams

6. THEORY

Beam: A bar subject to forces or couples that lie in a plane containing the longitudinal axis of the bar is called a beam. The forces are understood to act perpendicular to the longitudinal axis.

The most economical beam is the one with least cross-sectional area and consequently the least weigh per foot of length. In general, for a given area, a deeper beam is stronger than a shallower one.

DEPARTMENT OF CIVIL ENGINEERING

Bending Moment: The algebraic sum of the moments of the external forces to one side of any cross-section of the beam about an axis through that section is called the bending moment at that section.

Type of Bending: If couples are applied to the ends of the beam and on forces acts on the bar, then the bending is termed pure bending. For example, in Figure 2 the portion of the beam between the two downward forces is subjected to pure bending. Bending produced by forces that do not form couples is called ordinary bending. A beam subject to pure bending has only normal stresses with no shearing stresses set up in it; a beam subject to ordinary bending has both normal and shearing stresses acting within it.

Neutral Surface: There always exists one surface in the beam containing fibers that do not undergo any extension or compression, and thus are not subject any tensile or compressive stress. This surface is called the neutral surface of the beam.

Neutral Axis: The intersection of the neutral surface with any cross-section of the beam perpendicular to its longitudinal axis is called the neutral axis.

Navier’s Assumption: States that “plane section (normal to neutral axis) before bending remains plane after bending”.

Theory of Simple Bending: Bending is usually associated with shear. However, for simplicity we neglect the effect of shear and consider moment alone to find the stresses due to bending (i.e. bending stress). Such a theory which deals with finding stresses at a section due to pure moment is called simple bending theory.

Assumptions in theory of Simple Bending: The following assumptions are made in simple theory of bending:

(1) The beam is initially straight and every layer of it is free to extend or contract & bends into a circular arc

(2) The material is a homogeneous, isotropic & elastic continuum

(3) Young’s Modulus is same in tension and compression.

(4) The beam material obeys Hooke’s law and stresses are within elastic limits.

(5) Plane section remains plane even after bending

(6) The radius of curvature is large compared to depth of beam

(7) Beam deformation due to shear effects is neglected

(8) Effects of localized (concentrated) loads are neglected

(9) The beams bends about one of its principal axes

(10) Stresses are induced only in the longitudinal direction of the beam

For a simply supported beam with central loading, deflection under the load is given by

Where,

P = Applied load.

L = Effective span of the beam.

E = Modulus of Elasticity of wood.

I = Moment of inertia

δ = Mid-span deflection under the load.

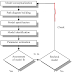
7. PROCEDURE

i) Measure all dimensions of the beam.

ii) Place the beam in proper position and apply load.

iii) Record the load at certain interval.

iv) Record the peak load from the load cell display of UTM machine.

v) Note the characteristics of the fractured surface.

8. EXPERIMENTAL SETUP

11. GRAPHS

1. Load vs. deflection curve of beam with higher I.

2. Load vs. deflection curve of beam with lower I.

3. Combined Load vs. deflection curve of beam with higher and lower I.

4. Draw SFD and BMD for the beams.

12. RESULT

(Students will fill up this section with their individual outcome/result about the test.)